Numerical Differential Equations
數值微分方程

Fall 2007


Jinn-Liang Liu

高雄大學應數系

All projects and home works should be submitted before 1/11/2008 (Friday).
None will be accepted after this date.

 

Homework 3. (Due 12/20)
Derive in details from 2D Poisson’s (strong) problem with zero Dirichlet boundary condition to its weak problem by using 2D divergence theorem.

Project 7. (Due 12/13)
Do Project 7.1 (CG).

Homework 2. (Due 11/29)
A. A complex square matrix A is a normal matrix if

A*A=AA*

where A* is the conjugate transpose of A. (If A is a real matrix, A*=AT and so it is normal if ATA = AAT.)  Show that if A is normal then the condition number

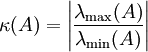
\kappa(A) = \left|\frac{\lambda_\max(A)}{\lambda_\min(A)}\right| 

where \lambda_\max(A),\ \lambda_\min(A) are maximal and minimal eigenvalues of A respectively.  Give an example for this theorem with a 3 by 3 matrix.

 

B. Prove the convergence result (7.23) in Lecture 7 for the method of steepest descent.
Write your homework in English and email it in pdf file to me.

 

Project 6. (Due 11/15)
Do Projects 4.1 (GS), 5.1 (SOR), and 6.1 (SSOR).

Homework 1. (Due 10/18)
A. Give a detailed analysis on the convergence order  (alpha) in (2.3) of Lecture 2. (Hint: Taylor’s Theorem)
B. Explain why (under what conditions) JM will converge. (Hint: Spectral analysis on the matrix B in (3.11) of Lecture 3.)
Write your homework in English and email it in pdf file to me.

 Project 5. (Due 10/11)
Do Project 3.1 (JM) in Lecture 3.

 Project 4. (Due 10/1)
Do Project 2.1 (GE) in Lecture 2.
Submit all files including I/O files. (From this project on.)

   

課程大綱

Lecture 1.  1D Poisson's Equation and Finite Difference Method (FDM)   

Lecture 2.  Gaussian Elimination (GE) for Ax=b  

Lecture 3.  Jacobi’s Method (JM)

Templates for the Solution of Linear Systems   (pdf)

Lecture 4.  Gauss-Seidel Method (GS)    

Lecture 5.  Successive Overrelaxation Method (SOR)   

Lecture 6.  Symmetric Successive Overrelaxation Method (SSOR)  

Lecture 7.  Conjugate Gradient Method (CG)  

Lecture 8.  Finite Element Method (FEM) for 1D Poisson’s Problem   

Lecture 9.  2D and 3D Poisson's  Equation

Lecture 10.  Convection-Diffusion-Reaction Model

Lecture 11.  1D Sturm-Liouville problem  (pdf*)

Lecture 12.   Power Method A (pdf*) Power Method B (pdf**)

Lecture 13.  QR METHOD A (pdf*)

Lecture 14.  A Brief Tour of Eigenproblems

 

教學目標

·         Learn basic numerical methods in Partial Differential Equations (PDEs)

·         Learn basic numerical methods in Numerical Linear Algebra

·        Learn basic Physics behind PDEs

·        Learn C++ programming in scientific computing

授課方式

·        Regular Lecturing

評分標準

·        Programming projects 60%

·        Homework 30%

·        In class performance 10%

教科書

·        Jinn-Liang Liu, Lecture Notes on Scientific Computing, 2007. 

閱讀文獻

·      [BB94] R. Barrett, M. Berry, T. F. Chan, J. Demmel, J. Donato, J. Dongarra , V. Eijkhout, R. Pozo, C. Romine, and H. Van der Vorst, Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd Edition, SIAM, 1994, Philadelphia, PA.

·      [BD00] Z. Bai, J. Demmel, J. Dongarra, A. Ruhe, and H. van der Vorst, editors. Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide. SIAM, Philadelphia, 2000.

·      [S00] Y. Saad, Iterative methods for sparse linear systems, 2000.

·      [S94] J. R. Shewchuk, An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, 1994.